Matrix Multiplication

The Kalman filter equations have many matrix multiplication operations. Actually, every equation involves a matrix multiplication operation.

Matrix multiplication is different than matrix addition or subtraction. In matrix addition, you took an element from the first matrix, found the matching element in the second matrix, and outputted the sum.

You can multiply matching elements in a matrix as well, but that is called element-wise multiplication. Matrix multiplication is a different operation. And matrix multiplication is trickier to code.

Multiplication of Matrix
\mathbf{A}
with matrix
\mathbf{B} is only possible if the number of columns in
\mathbf{A} is equal to the number of rows in
\mathbf{B}. So if matrix \mathbf{A} is
m \times n, then \mathbf{B} needs to be n \times p. The values for m and p can be any positive integer.

The result of \mathbf{A} \times \mathbf{B} is a matrix of size m \times p.

Formal Definition of Matrix Multiplication

Here is the formal equation for multiplying two matrices together:

(\mathbf{AB}){ij} = \sum{k=1}^n a_{ik}b_{kj}

All this is saying is that to find the element (i,j) in the resulting matrix, you need to

• take row i in matrix A, column j in matrix B
• do element-wise multiplication on the i-row A vector and j-column B vector
• sum the resulting elements

But you have already done element-wise multiplication and then summed the resulting elements of two vectors. That was the definition of the dot product in the vectors part of the lesson! Think of a matrix row as a vector and a matrix column also as a vector; you already wrote code for calculating the dot product.

So you are already part way done with coding matrix multiplication!

Let's go through a concrete example to see how matrix multiplication works. The two matrices being multiplied are:

\begin{bmatrix}17 & 25 & 6 & 2 \\6 & 1 & 97 & 4 \\80 & 8 & 54 & 15\end{bmatrix} \times\begin{bmatrix}3 & 14 & 1 & 7 & 42 & 5 \\32 & 11 & 2 & 4 & 18 & 17 \\19 & 81 & 4 & 8 & 5 & 10 \\27 & 2 & 3 & 6 & 7 & 3\end{bmatrix}= \begin{bmatrix}1019 & 1003 & 97 & 279 & 1208 & 576 \\2001 & 7960 & 408 & 846 & 783 & 1029 \\1927 & 5612 & 357 & 1114 & 3879 & 1121\end{bmatrix}

Note that matrix \mathbf{A} has three rows and four columns (3 x 4) and matrix \mathbf{B} has four rows and six columns (4 x 6). So the output is a 3 x 6 matrix.

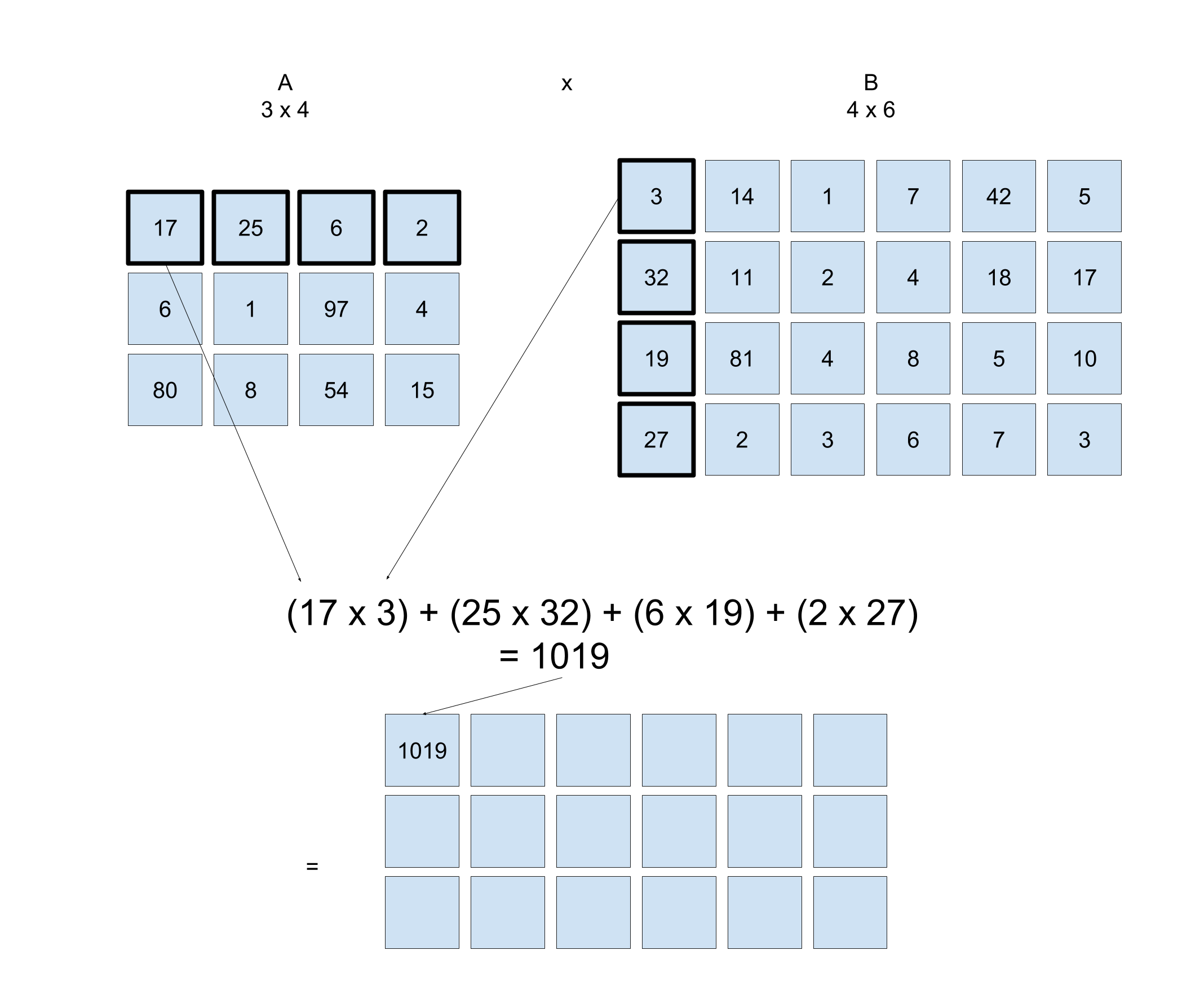
Where did the number 1019 come from in row one, column one? According to the formula for matrix multiplication, it came from element-wise multiplication of the first row of matrix \mathbf{A} with the first column of matrix \mathbf{B}.

Thus you calculate the dot product of row one of A and column one of B. The dot product involves element-wise multiplication and then summing the results:

\begin{bmatrix}17 & 25 & 6 & 2 \end{bmatrix}\cdot\begin{bmatrix}3 & 32 & 19 & 27\end{bmatrix}

= 17 \times 3 + 25 \times 32 + 6 \times 19 + 2 \times 27
= 1019

See the illustration below to see what is happening in more detail:

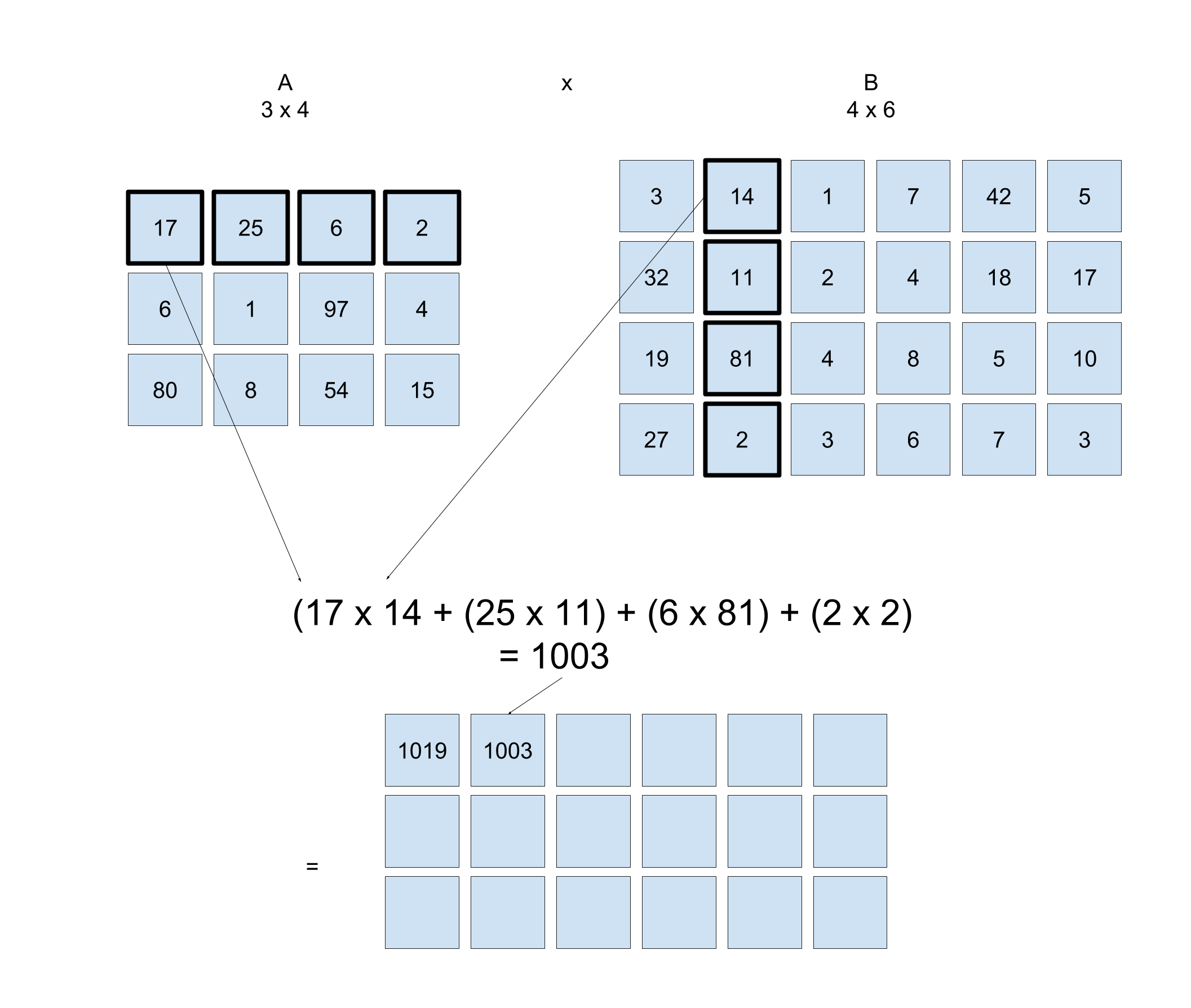
How would you calculate the value in row one, column two?

You can see in the visualization below how to calculate the value in row one, column two.

Jumping ahead, here is how you would calculate row two, column four. You would need the second row of matrix \mathbf{A} and the fourth column of \mathbf{B}.

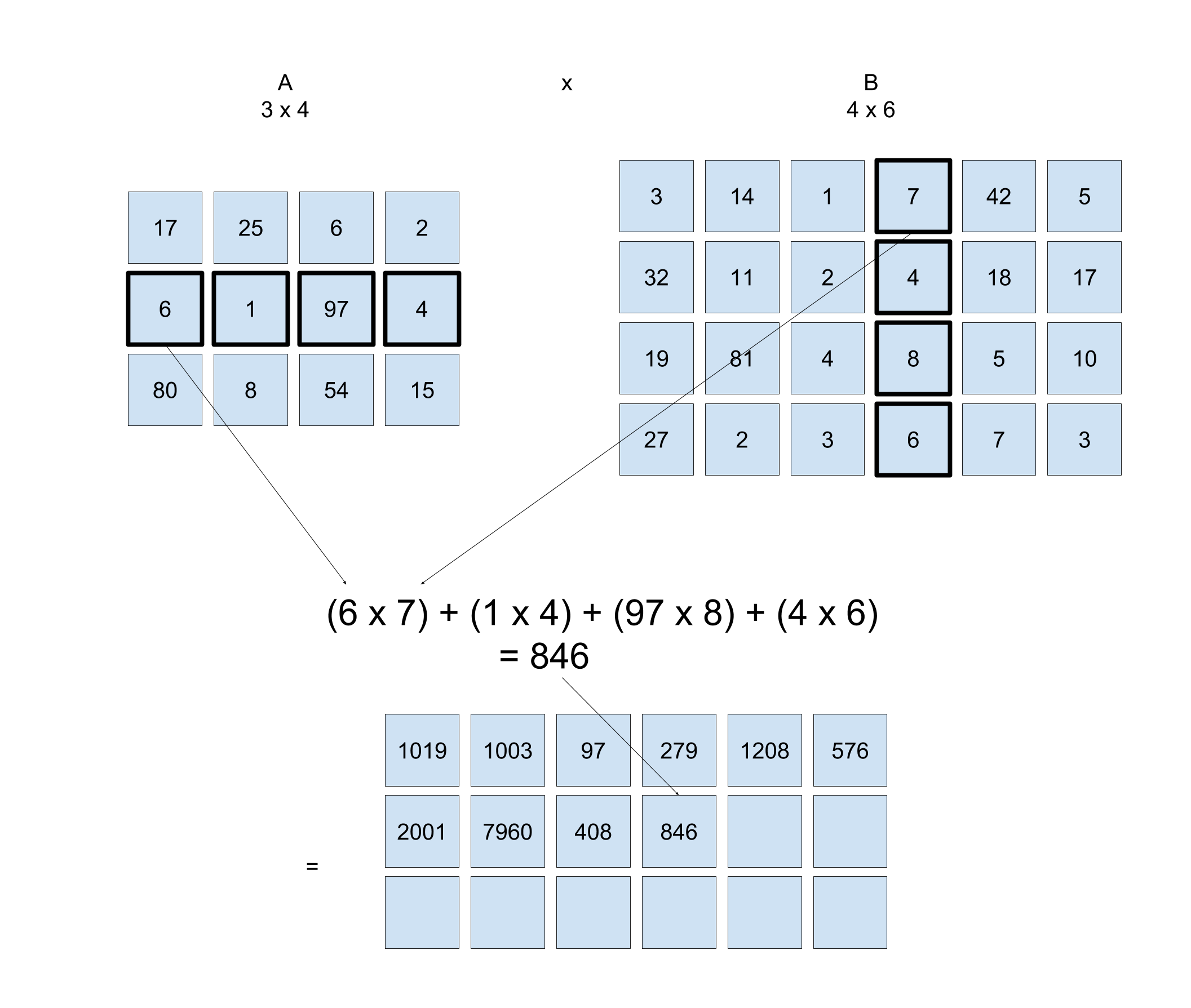
Continuing with the process, you end up with
\begin{bmatrix}1019 & 1003 & 97 & 279 & 1208 & 576 \\2001 & 7960 & 408 & 846 & 783 & 1029 \\1927 & 5612 & 357 & 1114 & 3879 & 1121\end{bmatrix}

Now it's your turn to code matrix multiplication in Python.

Coding Matrix Multiplication

Writing code for matrix multiplication can be quite tricky. So you are going to build the solution in pieces. The good news is that coding matrix multiplication is a big part of this module's final project.

Think about what matrix multiplication involves. You will multiply two matrices with sizes

• m x n
• n x p

and output a matrix of size m x p.

In previous exercises, you already iterated through matrices using nested for loops. How could you use a nested for loop to calculate each element in the m x p matrix? And then once you have grabbed the necessary row in A and the necessary column in B, how will you combine the values to get the right answer?

The next page has an Ipython notebook where you can write your code.